A new method of cloaking is presented by Fernando Guevara Vasquez, Graeme W. Milton, and Daniel Onofrei, Department of Mathematics, University of Utah.
For two-dimensional quasistatics it is proven how a single active exterior cloaking device can be used to shield an object from surrounding fields, yet produce very small scattered fields. The problem is reduced to finding a polynomial which is approximately one within one disk and zero within a second disk, and such a polynomial is constructed. For the two-dimensional Helmholtz equation, it is numerically shown that three active exterior devices placed around the object suffice to produce very good cloaking.
Recent proposals for invisibility, can be broadly placed in two main groups: interior cloaking, where the cloaking device surrounds the object to be cloaked, and exterior cloaking, where the cloaking region is, surprisingly, outside the cloaking device.
Interior cloaking methods include plasmonic cloaking due to scattering cancellation, transformation based cloaking, and active cloaking. Transformation based cloaking has gained particular attention, being supported by experiment and rigorous mathematics. While difficult to exactly achieve, various approximate schemes make it more practical.
Exterior cloaking methods include cloaking due to anomalous resonance where polarizable dipoles, and polarizable line quadrupoles, and clusters of arbitrarily many polarizable line dipoles in the vicinity of a flat or cylindrical superlens are cloaked, but apparently not larger objects, and cloaking due to complementary media where an “antiobject” is embedded in a superlens, to create cancellation.
Miller found that active controls rather than passive materials could be used to achieve interior cloaking. Here we use active cloaking devices to achieve exterior cloaking. In principle this could be done by mimicking the effect of the cloaking device of, but our objective is to have an active cloaking device which does not require one to know the shape of the object to be cloaked. Perhaps an analogy with water waves can be made. Our objective is to use the cloaking devices to create an area of still water, near but outside the cloaking devices, without disturbing the pattern of waves a certain distance away. Then a boat can be placed in the area of still water, without disturbing the surrounding waves: the boat is cloaked, and so
are the cloaking devices. The area of still water is created by destructive interference between the surrounding waves and anomalously localized waves created by the cloaking devices. Our cloaking approach has the disadvantage that one needs to
know in advance the incoming probing waves.
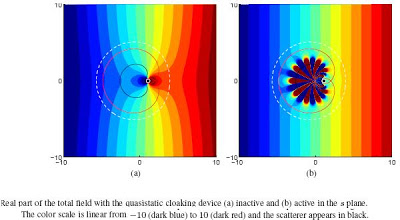
As shown on the right above. when the cloaking devices are active they create a “quiet” region where the wave field is close to zero. An object lying in this region is practically invisible because both the scattered and device’s fields are for all practical purposes undetectable outside of the dashed white circle. The field outside the dashed white circle is nearly identical to the incident plane wave: the discrepancy on that circle is of about 1:5 X 10^-5% of the incident field or 6:8 X 10^-5% of the uncloaked scattered field, measured with the L2 norm. Of course these relative errors depend on the particular choice of the cutoffs for the singular values in our two step approach.
A complete mathematical discussion, including the rigorous analysis for the arguments for the quasistatic case, together with a different analytical approach, will be included in a forthcoming publication. The theory for the Helmholtz problem remains an object of current research. We anticipate that the results extend to three-dimensions and to the full Maxwell equations but this remains to be explored.

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.