Improving Space Elevators By Having a Rototating Hoop

By have a rotating hoop for a space elevator then objects sliding along Rotating Space Elevator(RSE) strings do not require internal engines or propulsion to be transported from the Earth’s surface into outer space. (H/T Tom Craver)

A previous article had noted that the strength of the space elevator tether and the power of the engines driving the climbers were inter-related in terms of how feasible the space elevator was. By removing the need for powered climbers this could improve the overall feasibility of space elevators.

Physorg has info as well

To initiate the double rotational motion, the string system is given an initial spin. Other than this initial spin, the RSE moves purely under the influence of inertia and gravity. In simulations, Golubović and Knudsen show how a load starting at rest near the Earth spontaneously oscillates between its starting point near Earth and a turning point in outer space (close to the top of the string). Using a specially chosen variation of the tapered elevator cable cross-sectional area, the scientists could ensure that the RSE string will indefinitely maintain its initial looped shape. Golubović said that, as far as he knew, this type of motion does not occur in any other areas of physics or astronomy.

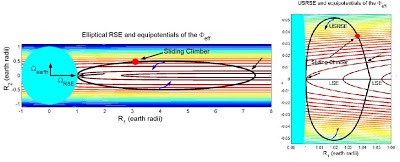
Golubović and Knudsen also proposed a slightly different form of the RSE, which combines an RSE with an LSE (an ellipse-like rotating string is attached to a linear string). This “uniform stress RSE” (USRSE) could be designed with its loop positioned above the Earth’s surface, which might have advantages for launching satellites. The scientists also show that stacking several USRSE loops could create pathways reaching deeply into outer space, and loads could cross from string to string at intersection points.

The RSEs are rapid outer space transportation systems that require no internal engines for the climbers sliding along the elevator strings. RSE strings exhibit interesting nonlinear dynamics and statistical physics phenomena. RSEs’ action employs basic natural phenomena—gravitation and inertial forces. Satellites and spacecrafts carried by sliding climbers can be released (launched) along RSEs. RSE strings can host space stations and research posts. Sliding climbers can be then used to transport useful loads and humans from the Earth to these outer space locations.

Strings and membranes play prominent roles in modern days investigations in statistical physics, nonlinear dynamics, biological physics, and in applied physical sciences. Technologically achievable celestial-size strings are no exception to this. Ever since an early dream of Tsiolkovsky, the vision of Space Elevator, a giant string connecting the Earth with heavens has intrigued diverse researchers as well as science fiction writers. The space elevator reaches beyond the geosynchronous satellite orbit. In its equilibrium state, the space elevator is straight and at rest in the non-inertial frame associated with the rotating planet, thanks to a balance between the gravity and the centrifugal force acting on the long elevator string. A major shortcoming of this traditional linear space elevator (LSE) is that significant energy must be locally (by internal engines, propulsion, or laser light pressure) supplied to climbers creeping along the LSE string to allow them to leave the gravitational potential trap of the Earth.

This study opens a new venue in the physics of strings and membranes. We introduce for the first time a novel class of nonlinear dynamical systems, Rotating Space Elevators (RSE). The RSEs are multiply rotating systems of strings. Remarkably, useful loads and humans sliding along RSE strings do not require internal engines or propulsion to be rapidly transported (sled) away from the Earth’s surface into outer space. The nonlinear dynamics and statistical physics of RSE strings are shown here to be also interesting in their own right.

Our RSE is a double rotating floppy string. In its quasi-periodic like state, the RSE motion is nearly a geometrical superposition of: a) geosynchronous (one-day period) rotation around the Earth, and b) yet another rotational motion of the string which is typically much faster (with period ~tens of minutes) and goes on around a line perpendicular to the Earth at its equator. This second, internal rotation plays a very special role: It provides the dynamical stability of the RSE shape and, importantly, it also provides a mechanism for the climbing of objects free to slide along the RSE string. The RSE can be envisioned in various shapes;. As revealed here, for a given RSE shape, by a special (magical) choice of the mass distribution of the RSE string, the simple double-rotating geometrical motion can be (under some conditions) made to represent an approximate yet exceedingly accurate solution to the exact equations of the RSE string dynamics.

Classical and statistical mechanics of celestial-scale spinning strings: Rotating space elevators (full 6 page article)

Figure 1. (Color online) In (a) and (d), respectively, the elliptical RSE and the USRSE (attached to a LSE) discussed in the text. In these figures we include also the equipotentials of the effective potential. Sliding climbers oscillate between two turning points (indicated by arrows) that are on the same equipotential. From our simulations: The R1(t) coordinate of the climber is shown in (b) and (e) on the floppy RSEs with initial shapes in, respectively, (a) and (d). (With a sliding friction (not included here), climbers would eventually stop at the RSE point minimizing the which occurs close to the RSE point with maximizing R2 in (a) and (d)). The magical mass distributions derived by eq. (8) are shown in (c) and (f) for the RSEs in, respectively, (a) and (d).